Floyed理解
Floyd算法的本质是动态规划,其转移方程为:f(k,i,j) = min( f(k-1,i,j), f(k-1,i,k)+f(k-1,k,j) )。
f(k-1,i,j)表示经过前k-1个点
f(k-1,i,k)+f(k-1,k,j)表示经过k这个点
f(k,i,j)表示路径除开起点i与终点j,只经过前k个点中的某些点,从i到j的最小值。
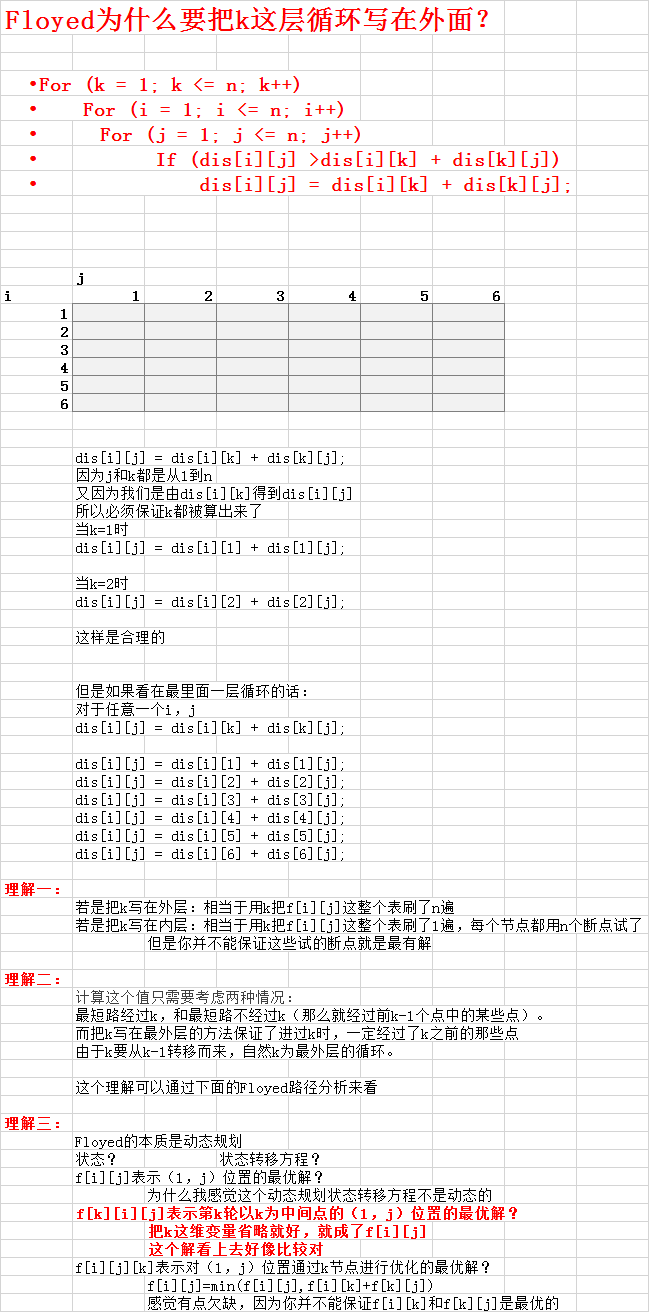
计算这个值只需要考虑两种情况:最短路经过k,和最短路不经过k(那么就经过前k-1个点中的某些点)。
由于k要从k-1转移而来,自然k为最外层的循环。而经过状态压缩(类似于背包问题)后,就变成了我们熟悉的f(i,j) = min( f(i,j), f(i,k)+f(k,j) )了。
接下来,是Floyd算法的更新过程。归纳一下它的更新过程,其实就是,每一次尝试在每一对节点Vv和Vw之间插入一个节点Vk,如果插入节点后,可以使得Vv和Vw之间的路径变短,那么进行一次更新,否则不更新。
那么,为什么按照这样的规则更新可以找到每对节点间的最短路径呢?我在这里举个例子说明一下,应该就可以把这个问题解释清楚了。假设我们事先已经知道从节点V2到V5之间的最短路径是:V2→V4→V9→V7→V5。
第一步,在初始化过程中,我们获得了(*D)[2][9]、(*D)[9][5]、(*D)[2][5]以及(*P)[2][9]、(*P)[9][5]、(*P)[2][5]的初始值。
第二步,按照Floyd算法进行迭代,迭代到k等于4时,我们会发现在V2和V9之间插入V4之后,V2和V9之间的路径长度达到了史上最低点,(*D)[2][9]更新为(*D)[2][4]+(*D)[4][9],(*P)[2][9]更新为4。而且在之后的迭代中都不会出现更短的路径,所以(*D)[2][9]和(*P)[2][9]在之后的迭代中都不会发生改变。
第三步,迭代到k等于7时,V9和V5之间的路径长度达到了史上最低点,(*D)[9][5]更新为(*D)[9][7]+(*D)[7][5],(*P)[9][5]更新为7,此后不再改变。
第四步,迭代到k等于9时,V2和V5之间的路径长度达到了史上最低点,(*D)[2][5]更新为(*D)[2][9]+(*D)[9][5],(*P)[2][5]更新为9,此后不再改变。这样也就找到了V2和V5之间的最短路径。
现在,我们算出了V2和V5之间的最短路径的长度,但是,怎样找到这条路径的轨迹呢?其实就是根据*P来推断。以上面的例子为例,如果我们要打印V2和V5之间的最短路径的轨迹。首先我们知道(*P)[2][5]=9,初步确定轨迹为V2→V9→V5。根据(*P)[2][9]=4且(*P)[9][5]=7,初步确定轨迹为V2→V4→V9→V7→V5。根据(*P)[2][4]=2,(*P)[4][9]=4,(*P)[9][7]=9,(*P)[7][5]=7,我们可以确定没有新的节点需要加入,所以确定最终的轨迹为V2→V4→V9→V7→V5。
Floyed题目推荐:
【P1119】灾后重建 - 洛谷
https://www.luogu.org/problem/show?pid=1119【P1078】文化之旅 - 洛谷
https://www.luogu.org/problem/show?pid=1078